In July 2013, a report titled "The Economic Benefits of Fixing our Broken Immigration System" was posted on the White House website. According to its second page, it was prepared by "the National Economic Council, the Domestic Policy Council, the President's Council of Economic Advisers and the Office of Management and Budget". On page 7, there appears the following statement:
Moreover, studies indicate that every foreign-born student with an advanced degree from a U.S. university who stays to work in a STEM field is associated with, on average, 2.6 jobs for American workers.
This statement references a summary of a 2011 working paper by Madeline Zavodny which links to the full paper titled "Immigration and American Jobs". Page 4 of this paper states that its analysis yielded the following findings on job creation:
Replication of Six Key Findings Using Study's Data and Shiny
Following is the statement that generates the regression from which the first key finding is derived. It is written in the Stata language and is taken from a file from the author named Tables1to3.do:
reg lnemprate_native lnimmshare_emp_stem_e_grad lnimmshare_emp_stem_n_grad i.statefip i.year [aw=weight_native] if year<2008, robust cluster(statefip)
This statement was replicated in the R language using the lm function. Also, to replicate the "robust cluster(metarea)" specification at the end of the Stata code above, it was necessary to use the sandwich package and the lmtest package as described in Option 1 at this link. The R code to replicate the key findings was used to create a dashboard using a framework called Shiny which can be used to see the effects of the various options used in the study. The code for this Shiny app can be found at this link and a running version of it can be accessed at https://econdata.shinyapps.io/amer_jobs1/. When run, the following initial screen is displayed:

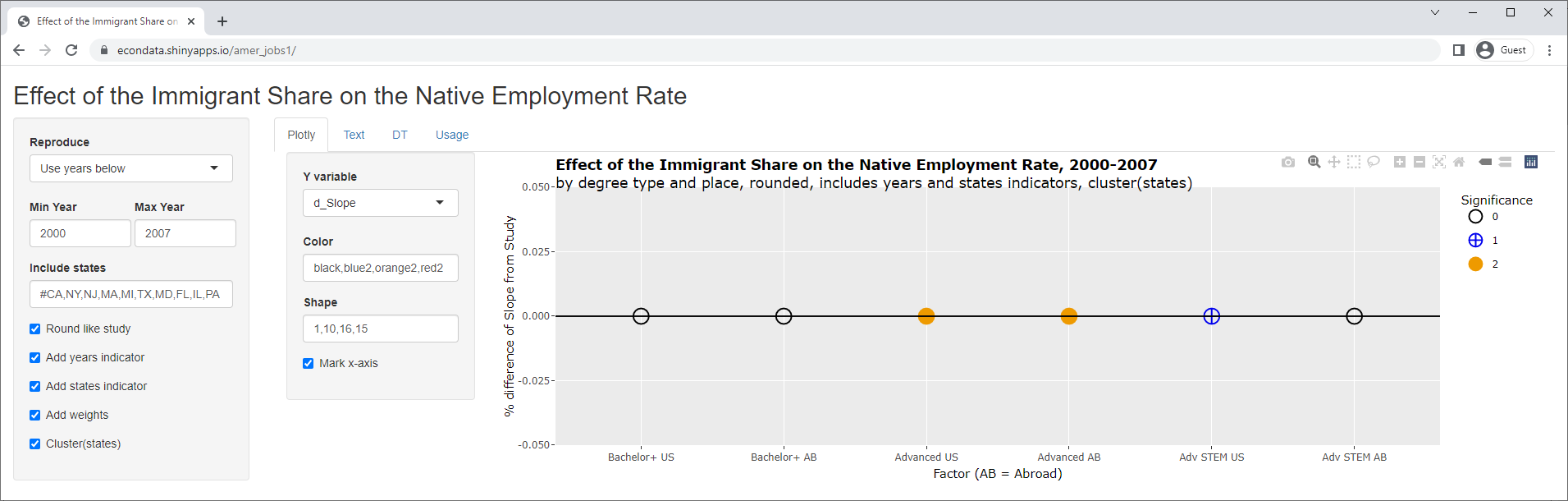
The plot shows the percent differences between the slopes of the reproduced regressions and the slopes of the regressions as reported in the study. The fact that the percents are all zero means the slopes were identical. This perfect reproduction does depend on the slopes being rounded to the same number of decimal places as the study. This was specified by checking the "Round like study" checkbox. Changing the select list "Y variable" to "d_Stderr" will show the same information (percent difference) for the standard errors:
As can be seen, all of the percents are zero indicating a perfect reproduction of the standard errors as well as the slopes. Clicking on the Text tab will display the following actual numbers:
Effect of the Immigrant Share on the Native Employment Rate, 2000-2007
by degree type and place, rounded, includes years and states indicators, cluster(states)
CALCULATED VALUES STUDY VALUES % DIFFERENCES DIFF
------------------------------------------------------------ --------------------- ---------------- ----
N INTERCEPT SLOPE STDERR TVALUE PVALUE SIG JOBS SLOPE STDERR SIG SLOPE STDERR SIG DESCRIPTION
-- --------- -------- ------- ------- ------- --- ------- ------- ------- --- ------- ------- --- -----------
1 4.1650 0.0030 0.0030 1.0542 0.2925 0 0.1535 0.0030 0.0030 0 0.0000 0.0000 0 Bachelor's Degree or higher, US
2 4.1650 0.0040 0.0030 1.3998 0.1625 0 0.1445 0.0040 0.0030 0 0.0000 0.0000 0 Bachelor's Degree or higher, Abroad
3 4.1798 0.0060 0.0030 2.4424 0.0151 2 0.7021 0.0060 0.0030 2 0.0000 0.0000 0 Advanced Degree, US
4 4.1798 0.0060 0.0030 2.2673 0.0240 2 0.6349 0.0060 0.0030 2 0.0000 0.0000 0 Advanced Degree, Abroad
5 4.1690 0.0040 0.0030 1.7522 0.0812 1 2.6299 0.0040 0.0030 1 0.0000 0.0000 0 Advanced Degree in STEM Occ, US
6 4.1690 -0.0002 0.0025 -0.0922 0.9267 0 -0.1019 -0.0002 0.0025 0 -0.0000 0.0000 0 Advanced Degree in STEM Occ, Abroad
As can be seen from the "% DIFFERENCES" columns, all of the reproduced slopes and standard errors are identical to those given in the study. The study's values all come from the OLS columns in Table 2 on page 20 of the study. The DIFF column shows that all of the signifcances of the p-values were identical as well.
The JOBS column in the prior table contains the value of 2.6299 for line 5, Advanced Degree in STEM Occupations, US. The Stata program files associated with this paper does not appear to contain its calculation. However, page 10 of the paper contains the following statement:
During 2000-2007, a 10 percent increase in the share of such workers boosted the US-born employment rate by 0.04 percent. Evaluating this at the average numbers of foreign- and US-born workers during that period, this implies that every additional 100 foreign-born workers who earned an advanced degree in the United States and then worked in STEM fields led to an additional 262 jobs for US natives. (See Table 2)
Assuming that dd contains the study's data for 2000-2007, the following is the calculation of "the average numbers of foreign- and US-born workers during that period":
foreign-born = sum(dd$emp_edus_stem_grad)/8 = 157289.6 US-born = sum(dd$emp_native)/8 = 103412351
It then appears that the number of jobs is calculated by truncating the following calculation:
jobs = 100 * slope * US-born / foreign-born = 100 * 0.004 * 103412351 / 157289.6 = 262.9859
This would make sense if the regression formula was the following:
emp_native = slope * emp_edus_stem_grad + ...
However, the actual regression formula is:
log(emprate_native) = slope2 * log(immshare_emp_stem_e_grad) + ...
which equals
log(100 * emp_native / pop_native) = slope2 * log(100 * emp_edus_stem_grad / emp_total) + ...
Hence, it is slope2 above that is measured as 0.004 and there is no clear reason to think that this will be equal to slope in the prior formula. That's especially the case since it contains pop_native (the native population) which should be largely unrelated to emp_native and emp_edus_stem_grad. In fact, some preliminary testing shows that the slopes will be nearly equal for small increases in employed compared to the current totals in employed. It's also necessary that pop_native not change significantly. If the population grows far faster than the number of jobs created, then the employment rate could drop despite the supposed job creation.
This brings up an issue that was discussed in section 6 at this link. As the name pop_native implies, it is including the entire native population, not just the labor force as is commonly done with employment rates.
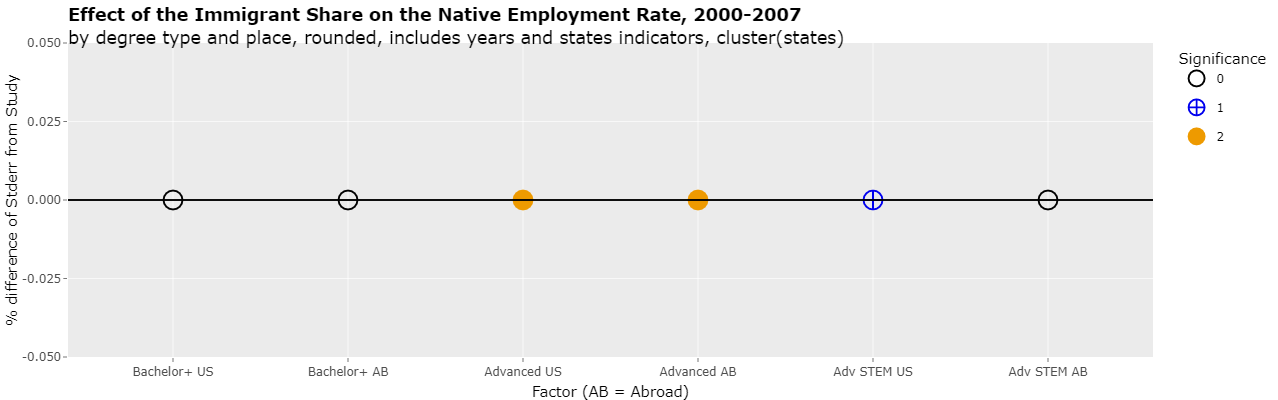
Clicking on the Plotly tab and changing the select list "Y variable" to "Pvalue" will show the actual p-values of the 6 regressions as following:
As can be seen, the 2nd regression is significant at the 1% level (less than 0.01) and the 3rd regression is significant to the 5% (less than 0.05) level. This is the same as was reported in the study.
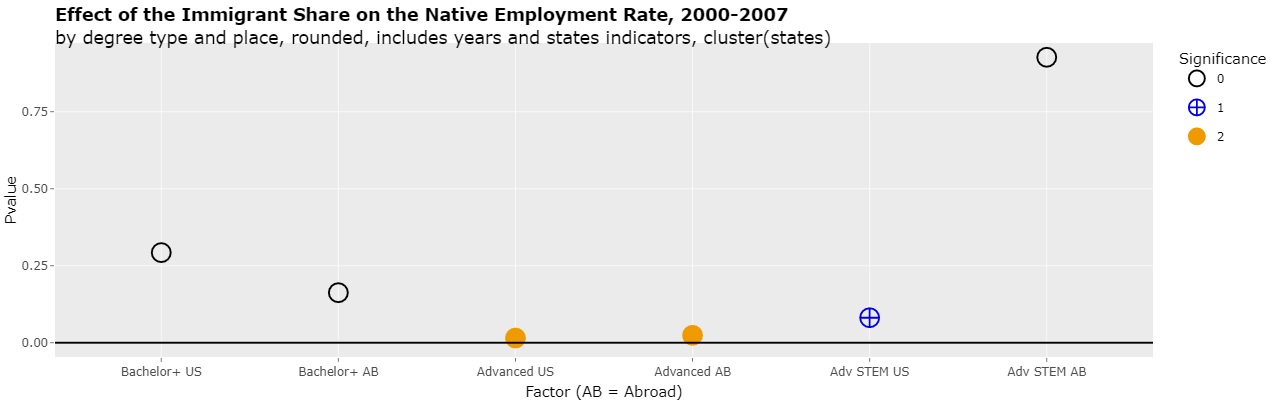
Changing the select list "Y variable" to "Slope" will show the actual slopes of the 6 regressions as follows:
Effect of Terms in the Regression Formula
The appendix of the paper on page 16 gives the regression formula and following description:
The basic empirical model estimated here is
with superscripts n indicating US natives and f indicating the foreign born, respectively, s indexing states, and t indexing years. The focus is on estimates of β which indicates how changes in the immigrant share of the employed affect the native employment rate. The δ terms are state and year fixed effects, and ε is a random error term. The error terms are robust and clustered on the state. Observations are weighted using the number of US natives in a state as a share of the total US native population that year. This gives each year the same total weight in the regressions. Regressions are estimated using ordinary least squares (OLS) or 2SLS, as discussed below.
The left side panel of the application contains checkboxes that allow terms or details in the regression formula to be turned on or off to see their effect. The screenshot below shows the effect of removing (by unchecking) the years indicator (described as "t indexing years" above):
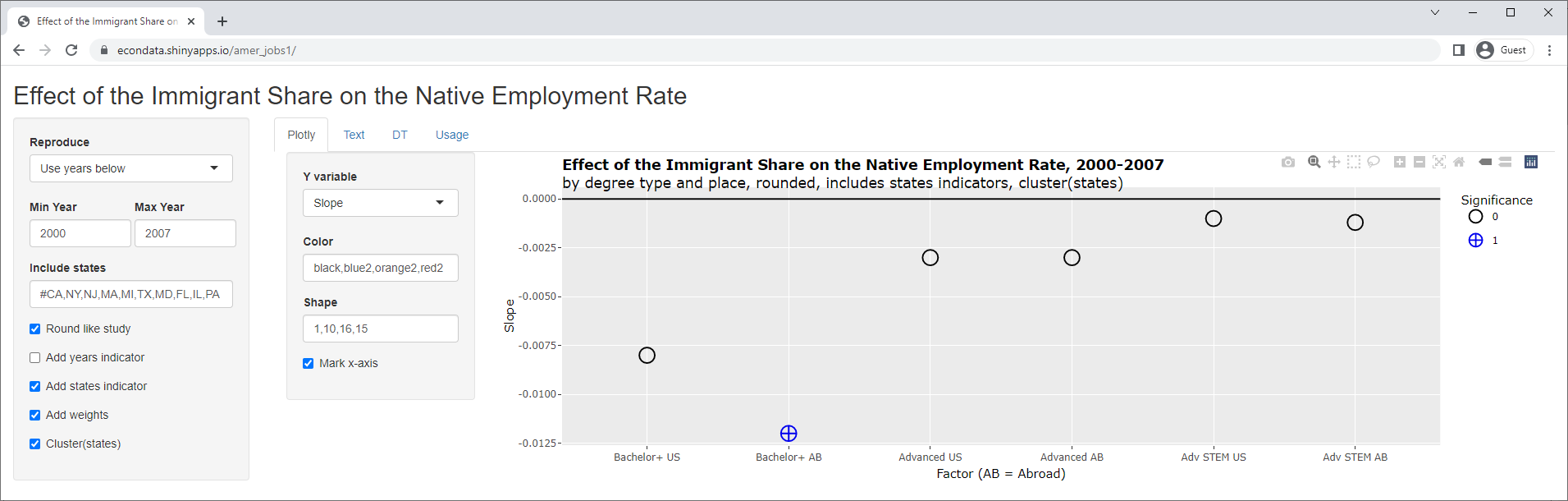
As can be seen, this causes a huge change with the slopes. As can be seen above, 5 of 6 of the slopes were positive but all are now negative. In addition, the 3 p-values that were significant are now insignificant and one of the 3 p-values that were insignificant is now significant. Removing the states indicator instead, results in the following:
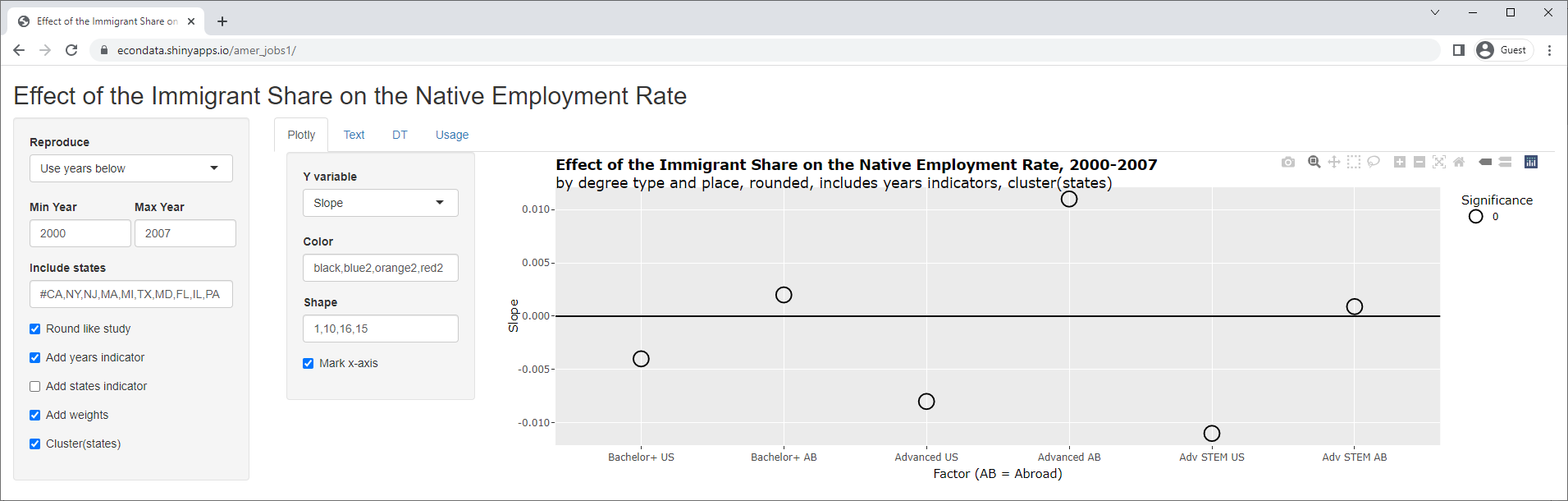
Now, 3 of the slopes are positive and 3 are negative. In addition, all of the p-values are now insignificant. Finally, also removing the clustering on the states results in the following:
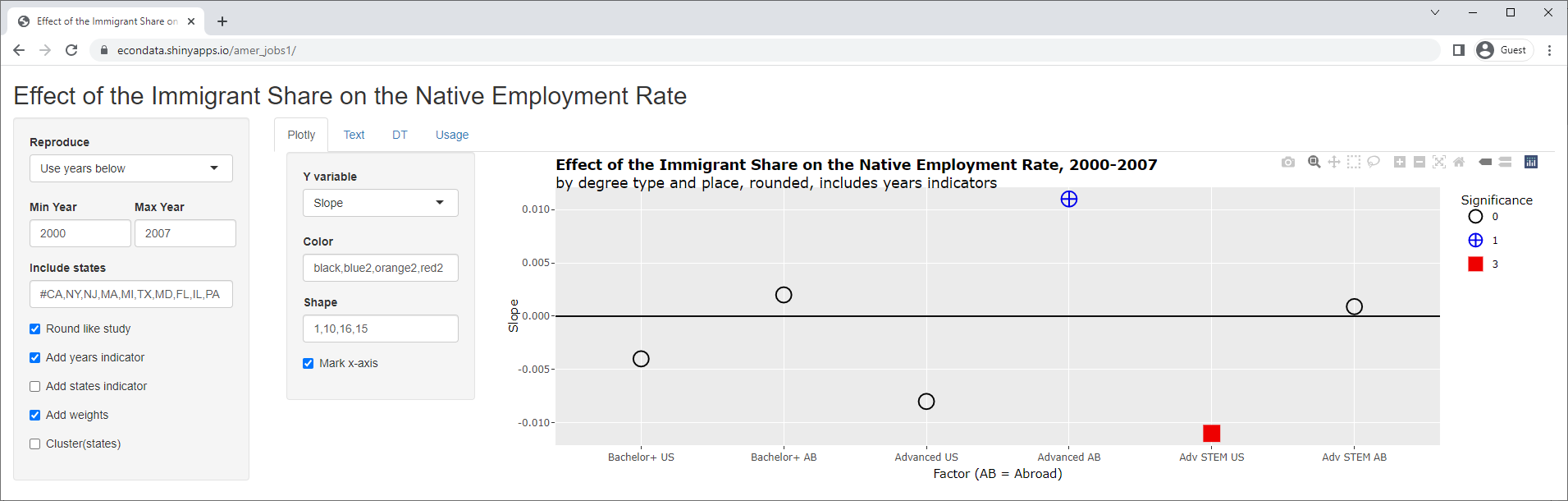
As can be seen, the slopes appear to all remain the same but two of them are now signficant. In fact, following are the outputs from the DT tab, with and without clustering:
Effect of the Immigrant Share on the Native Employment Rate, 2000-2007
by degree type and place, rounded, includes years indicators, cluster(states)
CALCULATED VALUES STUDY VALUES % DIFFERENCES DIFF
------------------------------------------------------------ --------------------- ----------------- ----
N INTERCEPT SLOPE STDERR TVALUE PVALUE SIG JOBS SLOPE STDERR SIG SLOPE STDERR SIG DESCRIPTION
-- --------- -------- ------- ------- ------- --- ------- ------- ------- --- -------- ------- --- -----------
1 4.2007 -0.0040 0.0110 -0.3503 0.7263 0 -0.2046 0.0030 0.0030 0 -233.3333 266.6667 0 Bachelor's Degree or higher, US
2 4.2007 0.0020 0.0120 0.2072 0.8359 0 0.0723 0.0040 0.0030 0 -50.0000 300.0000 0 Bachelor's Degree or higher, Abroad
3 4.2042 -0.0080 0.0100 -0.7972 0.4258 0 -0.9362 0.0060 0.0030 2 -233.3333 233.3333 -2 Advanced Degree, US
4 4.2042 0.0110 0.0090 1.1402 0.2549 0 1.1640 0.0060 0.0030 2 83.3333 200.0000 -2 Advanced Degree, Abroad
5 4.1823 -0.0110 0.0080 -1.3552 0.1765 0 -7.2321 0.0040 0.0030 1 -375.0000 166.6667 -1 Advanced Degree in STEM Occ, US
6 4.1823 0.0009 0.0086 0.1039 0.9173 0 0.4586 -0.0002 0.0025 0 -550.0000 244.0000 0 Advanced Degree in STEM Occ, Abroad
Effect of the Immigrant Share on the Native Employment Rate, 2000-2007
by degree type and place, rounded, includes years indicators
CALCULATED VALUES STUDY VALUES % DIFFERENCES DIFF
------------------------------------------------------------ --------------------- ----------------- ----
N INTERCEPT SLOPE STDERR TVALUE PVALUE SIG JOBS SLOPE STDERR SIG SLOPE STDERR SIG DESCRIPTION
-- --------- -------- ------- ------- ------- --- ------- ------- ------- --- -------- ------- --- -----------
1 4.2007 -0.0040 0.0060 -0.6060 0.5449 0 -0.2046 0.0030 0.0030 0 -233.3333 100.0000 0 Bachelor's Degree or higher, US
2 4.2007 0.0020 0.0070 0.3487 0.7275 0 0.0723 0.0040 0.0030 0 -50.0000 133.3333 0 Bachelor's Degree or higher, Abroad
3 4.2042 -0.0080 0.0050 -1.6372 0.1024 0 -0.9362 0.0060 0.0030 2 -233.3333 66.6667 -2 Advanced Degree, US
4 4.2042 0.0110 0.0060 1.7435 0.0821 1 1.1640 0.0060 0.0030 2 83.3333 100.0000 -1 Advanced Degree, Abroad
5 4.1823 -0.0110 0.0040 -2.8057 0.0054 3 -7.2321 0.0040 0.0030 1 -375.0000 33.3333 2 Advanced Degree in STEM Occ, US
6 4.1823 0.0009 0.0047 0.1885 0.8506 0 0.4586 -0.0002 0.0025 0 -550.0000 88.0000 0 Advanced Degree in STEM Occ, Abroad
As can be seen, clustering on states did not change the INTERCEPT or SLOPE (or JOBS, which depends on SLOPE) but did effect STDERR, TVALUE, PVALUE, and SIG.
Indicator Variables and Overfitting the Data
Regarding indicator variables, Wikipedia states the following:
In regression analysis, a dummy variable (also known as indicator variable or just dummy) is one that takes the values 0 or 1 to indicate the absence or presence of some categorical effect that may be expected to shift the outcome.
Regarding the years indicator variables, it's not entirely clear whether years would be best handled by an indicator variable or a continuous variable. The use of the states indicator variables raises a different question. Their use effectively adds a coefficient for every 8 data points, one for each state and Washington D.C. There would seem that there could be a danger of overfitting the data. In machine learning, this is tested for by cross-validation and/or by testing the model against out-of-sample data.
An article on overfitting in regression models states the following:
Harrell describes a rule of thumb to avoid overfitting of a minimum of 10 observations per regression parameter in the model. Remember that each numerical predictor in the model adds a parameter. Each categorical predictor in the model adds k-1 parameters, where k is the number of categories.
The data consists of 408 values (from the 8 years of 2000-2007 and the 50 states plus Washington D.C. mentioned above). The use of a categorical variable for the 50 states plus D.C. results in 50 (k-1) parameters being added. That's about 8 observations per regression parameter (408/50) versus the minimum of 10 suggested in the rule of thumb above. That would seem to raise the danger of overfitting.
At the very least, this shows the danger of using p-values as the primary indicator in a study. In fact, the American Statistical Association released a 2016 statement about p-values that warned about this. It listed six principles, the last of which was "By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis." Computer Science professor Norm Matloff blogged about this ASA statement at this link.
Testing the Model Against All Time Spans of 3 Years or More
One very straightforward way of validating the model is to test it against all time spans of some minimum length, say 3 years. Clicking on the DT tab displays the following:
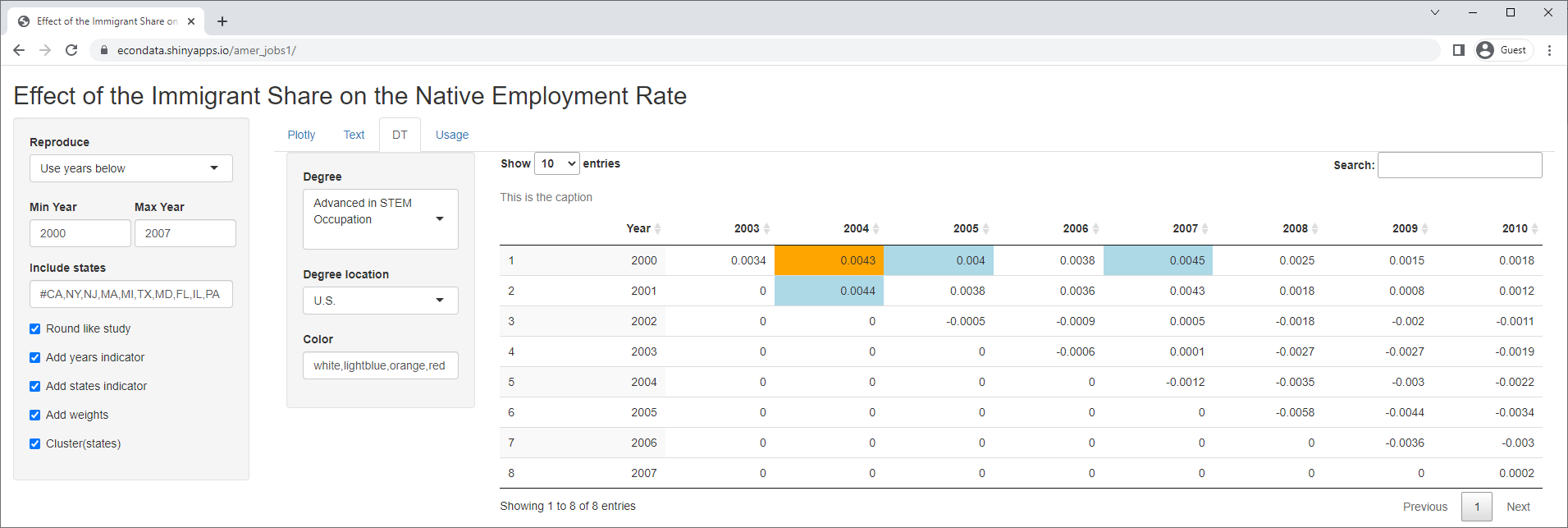
In this table, the levels of significance of 1 (< 10%), 2 (< 5%), or 3 (< 1%) are colored blue, orange, or red. The table contains 36 time spans of 3 years or more between 2000 and 2010. Of these, only 4 show any signficance using the study's model for foreign-born students with advanced degrees from U.S. universities. Now the study did only look at the years 2000 to 2007. The reason for this is recounted in a National Review article titled "The Myth of H-1B Job Creation". It states:
Zavodny's study initially examined data from the years 2000 to 2010. She hypothesized that states with more foreign-born workers would have higher rates of employment among native-born Americans. Initially, she was unable to find a significant effect of foreign-born workers on U.S. jobs.
So what changed? In correspondence with me and John Miano (the co-author of our new book, Sold Out, on the foreign-guest-worker racket), Zavodny revealed that when she showed her initial results to the study sponsor, the backers came up with the idea of discarding the last three years of data - ostensibly to eliminate the effects of the economic recession - and trying again.
Voilà! After recrunching the numbers at the sponsor's request, Zavodny found the effect the study sponsor was hoping to find.
However, the table shows that the 3 of the 4 significant time spans start in 2000 and the other one starts in 2001. Both years occurred in the dot-com crash which, according to Wikipedia, resulted in layoffs of programmers and a general glut in the job market. So if the job sponsors felt that 2008 to 2010 should be discarded, it would seem that 2000 to 2001 should be discarded as well.
As with the plotly charts, this table changes radically if some of the options are changed. For example, removing the states indicator variables and the clustering on the states results in the following table:
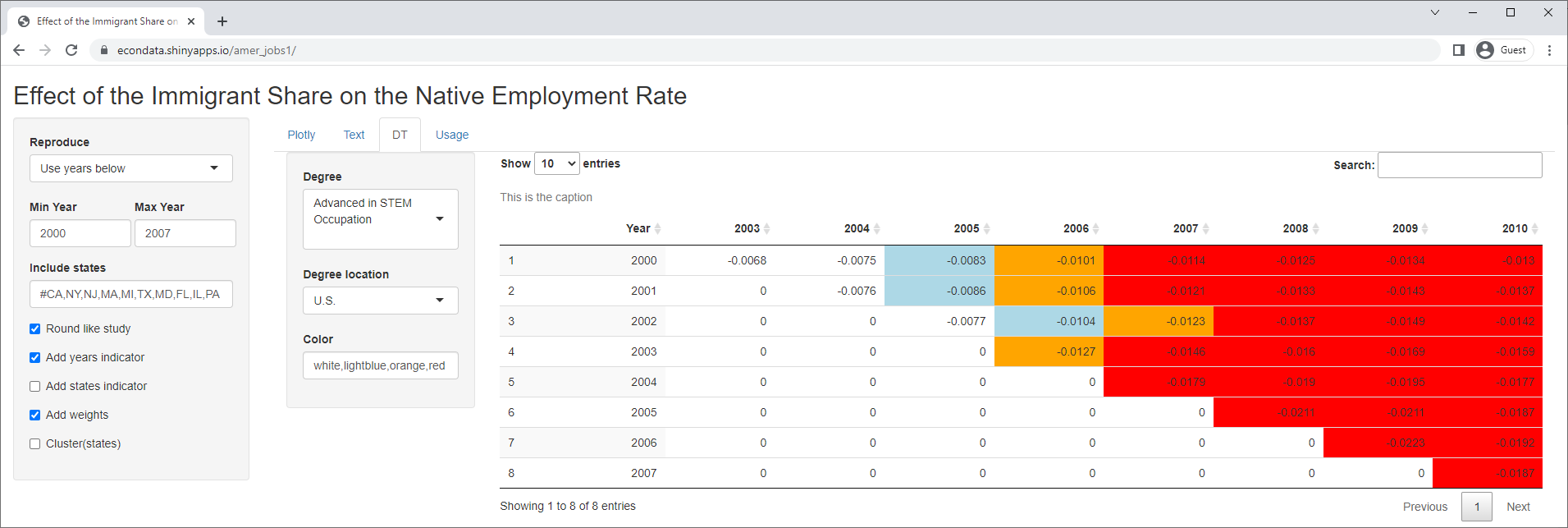
Now, the table shows highly significant p-values for nearly all time spans ending in 2007 or later. The fact that all of the slopes are negative means that this model finds strong evidence that foreign-born students with advanced degrees from U.S. universities cause job DESTRUCTION among native workers.
In any event, the fact that the study's model results in significant p-values in only 4 of 36 time spans indicates that there is little evidence to support it as a general model.