1. The Claim that Each Additional 100 H-1B Workers Create an Additional 183 Native Jobs
A study titled "Immigration and American Jobs", written by economist Madeline Zavodny, was released by the American Enterprise Institute and the Partnership For A New American Economy in December of 2011. On page 4 of this study, the second main finding states that "[a]dding 100 H-1B workers results in an additional 183 jobs among US natives." This is expanded upon on page 11 which states:
The estimates show that a 10 percent increase in H-1B workers, relative to total employment, is associated with a 0.11 percent increase in the native employment rate. During the sample period of 2001–2010, this translates into each additional 100 approved H-1B workers being associated with an additional 183 jobs among US natives.
The data used to reach this finding is explained on page 16 as follows:
The Department of Labor publishes data on applications for temporary foreign workers through the H-1B, H-2A, and H-2B programs. Those data are used here for the years they are available: 2001–2010 for the H-1B program, 2006–2010 for the H-2A program, and 2000–2010 for the H-2B program.[29] The measure of temporary foreign workers used here is the number of approved foreign workers in a given state and year. These counts of approved workers proxy for the ultimate number of new temporary foreign workers in each state, since data on actual temporary foreign worker inflows by geographic area are not available.[30]
Hence, the study is using the number of approved workers as proxy for the ultimate number of actual workers. In addition, this explanation refers to footnote 29 on page 23 which start as follows:
The data are from Foreign Labor Certification Data Center, www.flcdatacenter.com (accessed November 12, 2011), and are for fiscal years. The public-use H-1B data for 2007 contain erroneous codes for the work state, so the analysis here does not include that year.
For that reason, 2007 is likewise excluded for this replication. The following table shows the study's key H-1B data by year.
TABLE 1: H1B AND NATIVES: NUMBER EMPLOYED AND LEVELS, BY YEAR
year emp_h1b emp_native emp_total pop_native h1b_level nat_level ln_h1b_level ln_nat_level
---- --------- ----------- ----------- ---------- --------- --------- ------------ ------------
2001 1,432,702 102,771,951 119,489,933 155,359,951 1.1990148 66.15086 0.1815002 4.191938
2002 644,581 101,993,592 118,798,501 157,039,250 0.5425834 64.94783 -0.6114134 4.173584
2003 512,697 101,737,445 119,047,895 159,092,173 0.4306645 63.94874 -0.8424260 4.158082
2004 627,326 102,441,401 120,166,278 160,589,716 0.5220483 63.79076 -0.6499952 4.155608
2005 682,013 104,114,426 122,535,961 162,271,513 0.5565819 64.16063 -0.5859409 4.161390
2006 628,951 105,253,440 124,517,864 163,469,261 0.5051090 64.38730 -0.6829809 4.164916
2008 658,604 105,480,298 124,964,666 165,699,739 0.5270322 63.65749 -0.6404937 4.153517
2009 517,196 101,483,644 120,106,722 167,119,661 0.4306137 60.72514 -0.8425439 4.106358
2010 498,434 100,668,333 119,534,797 167,863,135 0.4169782 59.97048 -0.8747214 4.093852
Columns 2 and 3 are the number of employed h-1b and natives and columns 4 and 5 are the total employed and total native population. Columns 6 is the "h-1b level" and equals 100 times the employed h-1b (column 2) divided by the total employed (column 4). Column 7 is the "native level" and equals 100 times the employed natives (column 3) divided by the total native population (column 5). Columns 8 and 9 are just the logs of the levels in columns 6 and 7, respectively. These are the key numbers in the regressions.
As can be seen, employed h-1b (column 2) for 2001 is more than double its value for 2002 and later years. I looked at this several years ago and wrote the following at this link:
It should be noted that many applications did request just under 1,000 worker positions. I would assume that requests of 999 and slightly less often served as placeholders when large numbers of positions were desired but the exact number was unknown. The relatively large number of such requests in 2001 caused the total number of work positions to be over 1.4 million.
Because of this, the number of workers approved in 2001 may be far greater than the final actual number. In fact, the second table at this link shows that only 331,206 H-1B petitions were approved in 2001. Hence, the Labor Condition Applications (LCAs) may be a very poor proxy for the actual H-1B worker inflow per state since their is no guarantee that states will have similar ratios of certified to actual workers. Finally, it should be noted that this is only a proxy (likely a poor one) for the new H-1B workers. It reveals nothing about the cumulative number of such workers.
In any case, following table shows the results of regressions on the study's H-1B data:
[1] "TABLE 2: RESULTS OF REGRESSIONS ON STUDY'S H-1B DATA " [1] " " [1] " JOBS CORREL " [1] " N INTERCEPT SLOPE CREATED COEF DESCRIPTION " [1] "-- --------- -------- ------- ------- -----------------------------------" [1] "2001-2010, ALL DATA" [1] " 1) -0.3193 0.0219 326.4 0.2989 ln_nat_level ~ ln_imm_level" [1] " 2) -0.3227 0.0170 253.6 0.2989 ln_nat_level ~ ln_imm_level + fyear" [1] " 3) -0.4718 -0.0008 -11.5 0.2989 ln_nat_level ~ ln_imm_level + fyear + floc" [1] " 4) -0.3956 0.0110 182.5 0.2989 ln_nat_level ~ ln_imm_level + fyear + floc, weights=weight" [1] "USING STUDY'S FORMULA" [1] " 5) -0.3956 0.0115 171.6 0.2989 2001-2010, study's data with corrected job count" [1] " 6) -0.4265 0.0081 140.3 0.2439 2002-2010, skip bad data for 2001" [1] " 7) -0.4912 -0.0023 -37.6 0.2177 2002-2008, skip worse years of job loss" [1] " 8) -0.5230 -0.0064 -108.3 0.2142 2003-2006, skip all years of job loss" [1] " 9) -0.5716 -0.0132 -223.4 0.2450 2003-2005, longest span of growing h1b level"Regressions 1 to 4 show the results of the regression after adding each additional variable. The variable fyear is a dummy variable for year, floc is a dummy variable for the state, and weight is a weight used by the study. The weight is based on the native population of each state in each year. Regression 4 is the one on which the study's 183 number is based. However, it appears that Zavodny used the total number of H-1B workers from 2001 to 2010 but the total number of native workers from 2000 to 2010 for the calculation. She also used 0.011 for the slope instead of the exact slope, shown to be about 0.0115 above. After I corrected the calculation to use 2001 to 2010 for both H-1B and native workers and used the more precise measurement of slope, I got 171.6 for the calculated number of jobs created. Using the mismatched time spans and a slope of 0.11 like the study, I came up with 182.5, replicating the study. Similarly, the calculated slope of 0.0115 replicates the study's finding of 0.011 for the slope.
Regressions 5 to 9 show the results using the study's formula for different spans of years. The reason for looking at different spans of years is that the study claims to be looking at jobs being created due to an increase in the level of H-1B workers. It therefore makes sense to look at spans of years when the level of H-1B workers is rising. Certainly, one could claim that decreasing the level of H-1B workers has a negative effect on the native employment level. However, this occurred most severely after the 2001 tech crash and the 2008 financial crisis. The loss of jobs for both H-1B and natives was likely due to these economic events. In these events, I don't know that anyone would claim that the drop in H-1B workers was an independent event and that caused the drop in native employment. At the very least, there was likely a very different dynamic at work during these periods and they should be measured separately. In any event, the table shows that, when focusing on those years for which there were job gains for H-1B workers, those gains, on average, were correlated with drops in native employment, at least when using the study's own methodology.
The following table shows the slopes obtained for all spans of two or more years using the same formula that the study used to obtain the 183 figure. The figures in red are negative and indicate a negative correlation between H-1B and native employment level over the given time spans when using the study's methodology.
[1] "TABLE 3: SLOPE BETWEEN GIVEN YEARS (using same regression as was used to obtain 183 job finding)" [1] "---- ------ ------ ------ ------ ------ ------ ------ ------ ----" [1] "year 2003 2004 2005 2006 2007^ 2008 2009 2010 year" [1] "---- ------ ------ ------ ------ ------ ------ ------ ------ ----" [1] "2001 0.0071 0.0048 0.0014 0.0049 NA 0.0043 0.0104 0.0115 2001" [1] "2002 -0.0030 -0.0095 -0.0035 NA -0.0023 0.0069 0.0081 2002" [1] "2003 -0.0132 -0.0064 NA -0.0041 0.0061 0.0070 2003" [1] "2004 -0.0104 NA -0.0047 0.0084 0.0079 2004" [1] "2005 NA -0.0018 0.0097 0.0066 2005" [1] "2006 0.0010 0.0073 0.0009 2006" [1] "2007 -0.0192 -0.0152 2007" [1] "2008 -0.0152 2008"The following table shows the corresponding jobs gained or lost using the same formula that the study used to obtain the 183 figure. As previously mentioned, however, it appears that the study incorrectly uses 2000-2010 for the native employment instead of 2001-2010 as with H-1B employment. Also, the study appears to have truncated the above slopes to 3 decimal places as shown in Table 4 of the study. As before, the figures in red are negative and indicate a drop in native employment levels when using the study's methodology.
[1] "TABLE 4: JOBS GAINED/LOST BETWEEN GIVEN YEARS (with incorrect native employment in 1st row and truncation errors in all rows)" [1] "---- ------ ------ ------ ------ ------ ------ ------ ------ ----" [1] "year 2003 2004 2005 2006 2007^ 2008 2009 2010 year" [1] "---- ------ ------ ------ ------ ------ ------ ------ ------ ----" [1] "2001 110.7 63.7 15.8 63.7 NA 63.8 162.8 182.5# 2001" [1] "2001 82.8 50.8 13.2 54.6 NA 55.8 144.7 164.2* 2001" [1] "2002 -68.6 -166.3 -66.6 NA -49.6 101.5 138.1 2002" [1] "2003 -236.9 -118.1 NA -83.5 102.7 104.9 2003" [1] "2004 -177.0 NA -80.3 133.3 120.0 2004" [1] "2005 NA -32.0 150.7 103.9 2005" [1] "2006 0.0 121.1 0.0 2006" [1] "2007 -352.0 -294.0 2007" [1] "2008 -294.0 2008" # value is 182.5 if 2000-2010 is incorrectly used for total native employment and the slope is truncated. * value is 164.2 if 2001-2010 is correctly used for total native employment but the slope is truncated. ^ the study excludes 2007 stating "[t]he public-use H-1B data for 2007 contain erroneous codes for the work state, so the analysis here does not include that year."The following table shows the corresponding jobs gained or lost using the same formula that the study used to obtain the 183 figure but with no truncation or other errors. As before, the figures in red are negative and indicate a drop in native employment levels when using the study's methodology.
[1] "TABLE 5: NATIVE JOBS GAINED/LOST PER EACH 100 NEW H-1B WORKERS BETWEEN GIVEN YEARS (using the study's methodology with no errors)" [1] "---- ------ ------ ------ ------ ------ ------ ------ ------ ----" [1] "year 2003 2004 2005 2006 2007^ 2008 2009 2010 year" [1] "---- ------ ------ ------ ------ ------ ------ ------ ------ ----" [1] "2001 83.5 61.2 18.9 66.2 NA 59.4 150.6 171.6* 2001" [1] "2002 -51.5 -157.3 -59.0 NA -37.6 115.9 140.3 2002" [1] "2003 -223.4 -108.3 NA -68.6 104.2 122.2 2003" [1] "2004 -168.1 NA -76.2 139.1 135.7 2004" [1] "2005 NA -29.4 162.7 114.9 2005" [1] "2006 15.6 126.0 17.0 2006" [1] "2007 -338.8 -278.6 2007" [1] "2008 -278.6 2008" * value is 171.6 if 2001-2010 is correctly used for total native employment and the slope is not truncated. ^ the study excludes 2007 stating "[t]he public-use H-1B data for 2007 contain erroneous codes for the work state, so the analysis here does not include that year."The p-value is the standard method that statisticians use to measure the "significance" of their analyses. Wikipedia defines it as follows:
In statistics, the p-value is a function of the observed sample results (a statistic) that is used for testing a statistical hypothesis. Before performing the test a threshold value is chosen, called the significance level of the test, traditionally 5% or 1% [1] and denoted as alpha. If the p-value is equal or smaller than the significance level (alpha), it suggests that the observed data are inconsistent with the assumption that the null hypothesis is true, and thus that hypothesis must be rejected and the alternative hypothesis is accepted as true. When the p-value is calculated correctly, such a test is guaranteed to control the Type I error rate to be no greater than alpha.
Table 2 of the study showed that the regression on which the 2.6 job claim is made had a p-value such that 0.05 < p-value < 0.1. Following is one rough description of how to interpret a p-value:
0.10 < P No evidence against the null hypothesis. The data appear to be consistent with the null hypothesis.
0.05 < P < 0.10 Weak evidence against the null hypothesis in favor of the alternative.
0.01 < P < 0.05 Moderate evidence against the null hypothesis in favor of the alternative.
0.001 < P < 0.01 Strong evidence against the null hypothesis in favor of the alternative.
P < 0.001 Very strong evidence against the null hypothesis in favor of the alternative.
The following table shows the p-values that correspond to the regression slopes in the prior tables:
[1] "TABLE 6: P-VALUE OF REGRESSION SLOPE BETWEEN GIVEN YEARS (using study's methodology)" [1] "---- ------ ------ ------ ------ ------ ------ ------ ------ ----" [1] "year 2003 2004 2005 2006 2007 2008 2009 2010 year" [1] "---- ------ ------ ------ ------ ------ ------ ------ ------ ----" [1] "2001 0.16534 0.25727 0.71120 0.20737 0.20737 0.27447 0.01220 0.00697 2001" [1] "2002 0.62295 0.04438 0.43675 0.43675 0.61268 0.14819 0.08908 2002" [1] "2003 0.01225 0.21006 0.21006 0.42960 0.26340 0.19463 2003" [1] "2004 0.15324 0.15324 0.50799 0.23695 0.23302 2004" [1] "2005 0.19173 0.84628 0.25582 0.38787 2005" [1] "2006 0.96178 0.51965 0.91383 2006" [1] "2007 0.13328 0.10355 2007" [1] "2008 0.10355 2008"In the above table, p-values showing strong evidence (P < 0.01) are colored red, p-values showing moderate evidence (0.01 < P < 0.05) are colored orange, and p-values showing weak evidence (0.05 < P < 0.10) are colored green. Since this includes only 5 points, p-values that show close to weak evidence (0.10 < P < 0.20) are colored blue. In addition, p-values corresponding to negative slopes are in bold lettering.
As can be seen, the smallest p-values are for the spans 2001 to 2010, 2001 to 2009, 2003 to 2005, and 2002 to 2005. Oddly, the first two correspond to a positive slope and the latter two correspond to a negative slope. Even more oddly, the latter two spans are contained within the former two spans. Expanding upon this, it appears that those spans corresponding to a negative slope but having the lowest p-values are those spans which are 7 years or longer and/or which include 2001. However, those spans corresponding to a positive slope but having the lowest p-values tend to be for shorter spans.
One possible explanation for this apparent contradiction is revealed in Table 1. As can be seen, 2001 to 2002 included a massive drop in H-1B approvals with the number dropping by about 55 percent, from 1,432,702 to 644,581. This decline continued to 512,697 in 2003. The number of H-1B approvals then climbed strongly to 682,013 in 2005 and then stabilized somewhat dropping slightly to 658,604 in 2008. They then dropped sharply again, reaching 498,434 in 2010. As explained in the text after Table 1, the number of H-1B approvals may not be that good of a proxy for the number of H-1B workers. Still, if one is attempting to show the positive effects of an increase in H-1B workers, it would seem to make more sense to focus on periods when the number is actually increasing. As mentioned above, the longest period of strong growth in H-1B approvals was from 2003 to 2005. This period is associated with a negative growth and a p-value showing moderate evidence in favor of the alternative hypothesis that a growth in H-1B workers negatively affects the growth in native workers.
In summary, the entire span from 2001 to 2010 gives a low p-value corresponding with a POSITIVE slope but the spans 2002 to 2005, 2005 to 2007, and 2007 to 2010 show relatively low p-values corresponding with NEGATIVE slopes. This apparent contradiction may be due to attempting to fit a single model to periods when H-1B approvals are increasing and periods when H-1B approvals are decreasing. This may be essentially comparing apples and oranges. At the very least, this shows that selecting one time span and not bothering to look at other time spans is a deeply flawed approach.
2. An Initial Look at the Data
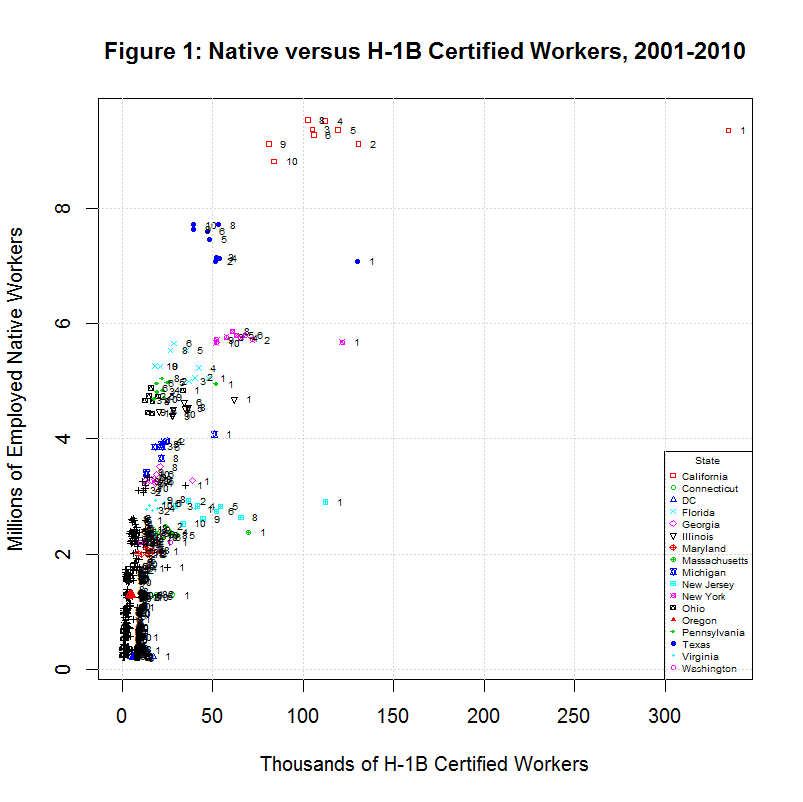
Before looking at the regression that led to the 183 number, it helps to look at the distribution of workers among the states in the following plot:

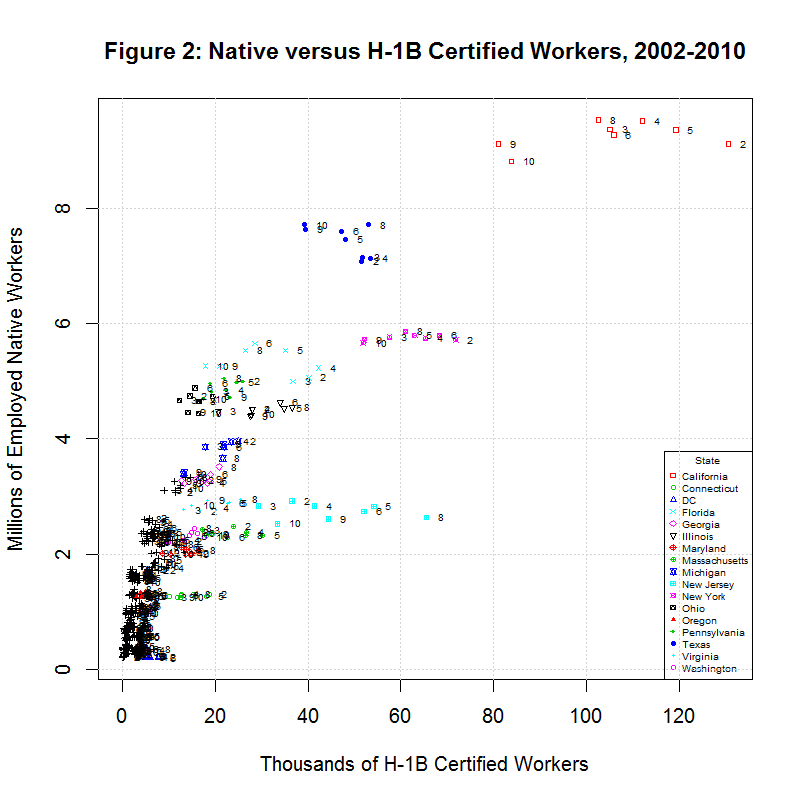
The numbers to the right of each point give the last digit of the year. As can be seen, many of the states have an extremely large number for H-1B workers for 2001. It's unclear what the exact cause of this was. In any event, the following plot omits 2001 so that the other data for other years is more visible:
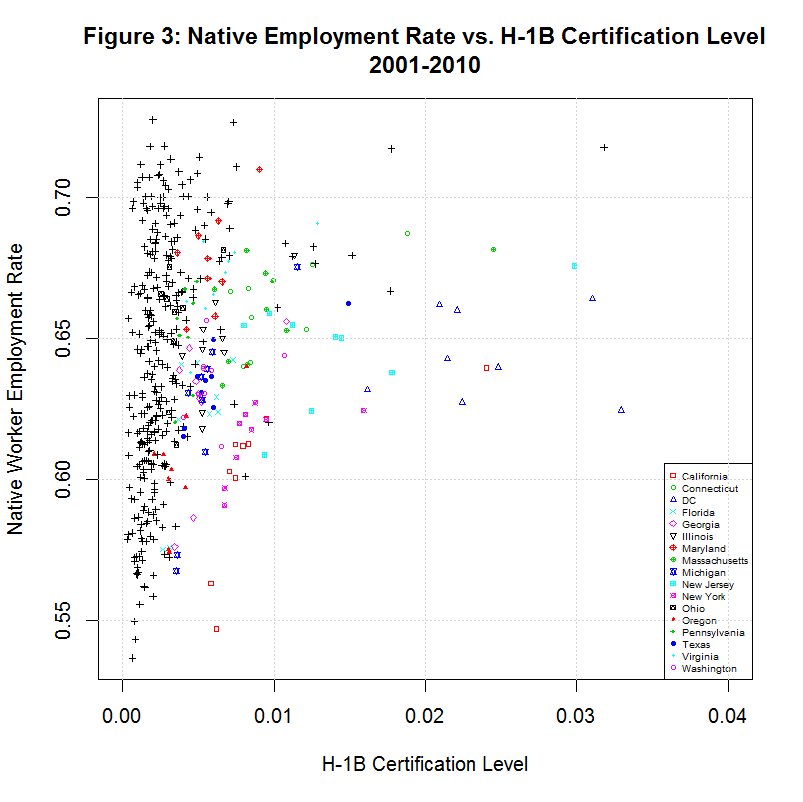
The following plot shows the native employment level verus the H-1B Certification level. Note that the native employment level averages around 65 percent. Hence, this is not the native employment rate but a measure of the native employment divided by the native population.
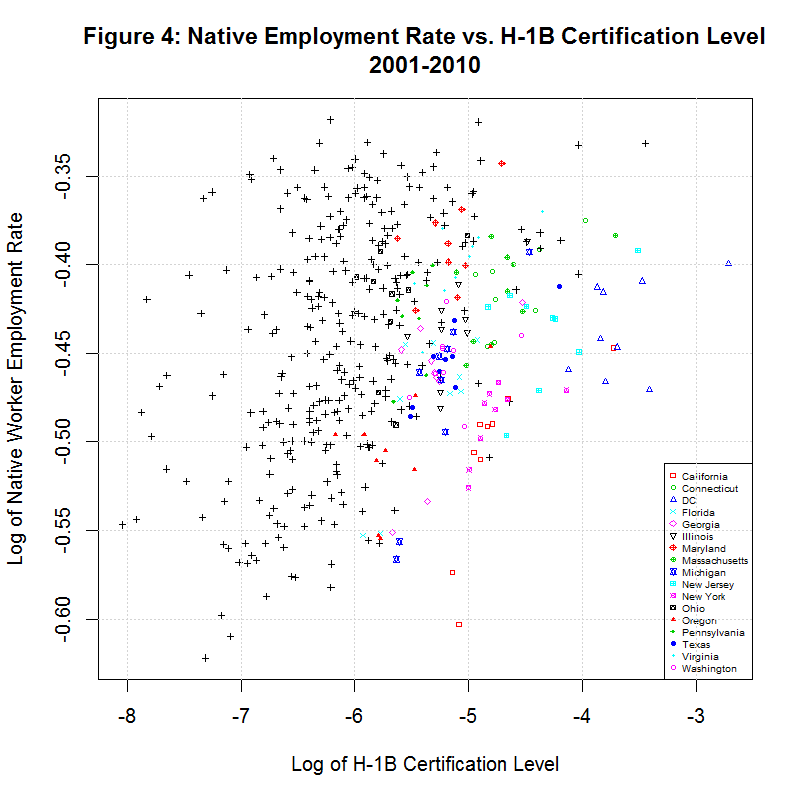
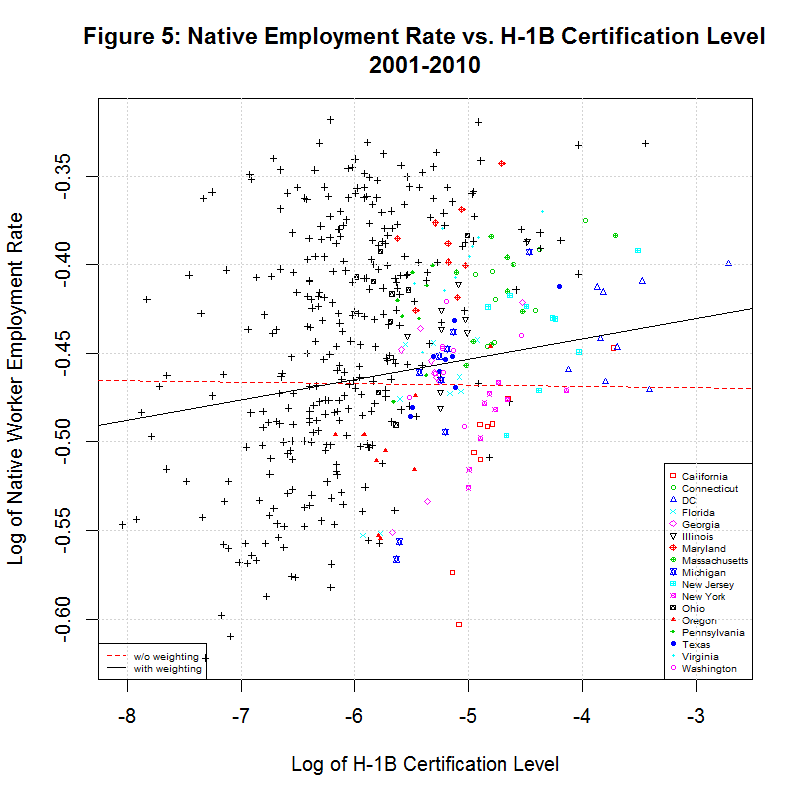
The following two graph show plots of the actual data that is being fit with a regression. The second of the plots show the weighted and unweighted regression of the data. The black line shows the weighted regression that was used by the study to calculate the 183 figure.
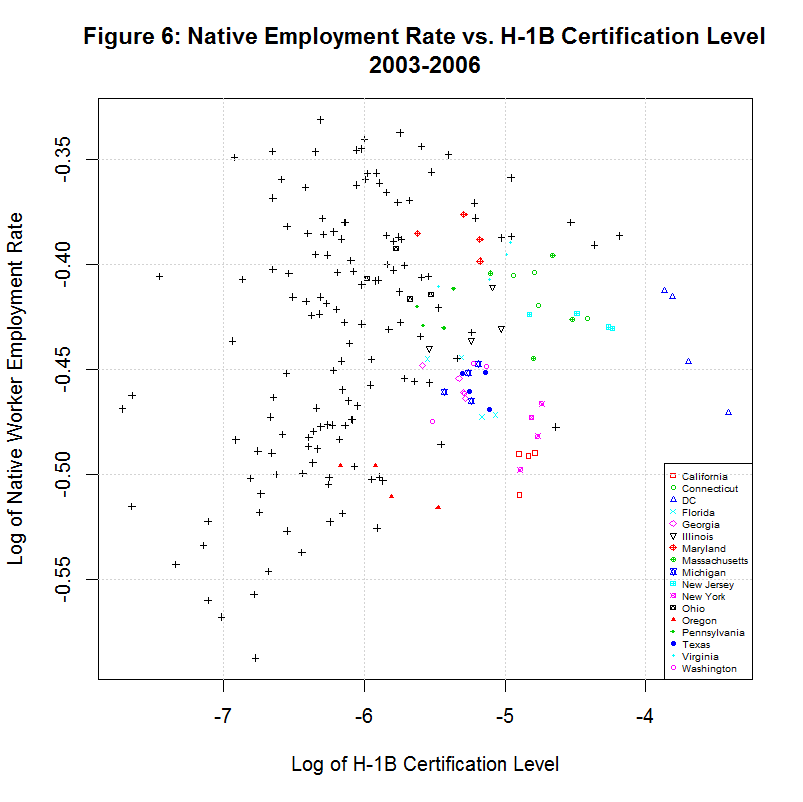
The following two graphs show the same data for 2003 to 2006, a time span when the H-1B level was generally increasing.
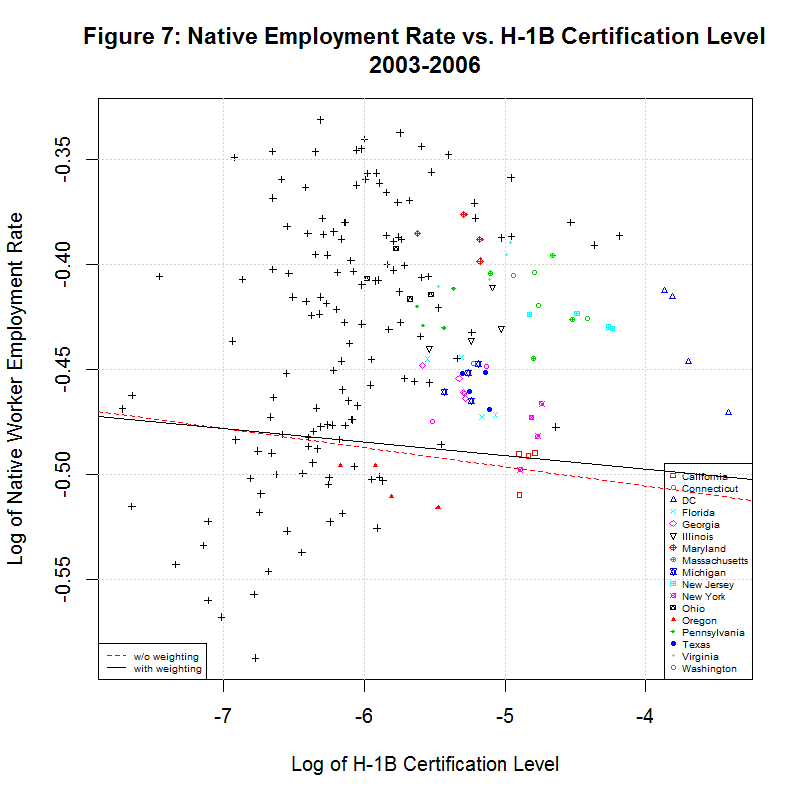
Note that both the weighted and unweighted lines show a negative slope, counter to the study's finding. It should also be noted that the lines do not seem appear to be the best fit of the data. This is caused by the fact that there are dummy variables in addition to the main independent and dependent variable. The cloud-like appearance of the data in these and the prior two graphs suggest that the data is not strongly correlated. However, it is difficult to judge the exact level of correlation since there are more than two variables.
All of the above arguments apply to the 262 number from the study as well. The following table shows the study's key data for this specific class of foreign STEM worker:
TABLE 7: FOREIGN-BORN STEM WORKERS WITH ADVANCED U.S. DEGREE: NUMBER EMPLOYED AND LEVELS, BY YEAR year emp_imm emp_native emp_total pop_native imm_level nat_level ln_imm_level ln_nat_level ---- -------- ----------- ----------- ----------- --------- --------- ------------ ------------ 2000 148,984 103,082,363 119,167,108 154,182,309 0.1250216 66.85745 -2.079268 4.202563 2001 141,657 102,771,951 119,489,933 155,359,951 0.1185521 66.15086 -2.132403 4.191938 2002 121,521 101,993,592 118,798,501 157,039,250 0.1022919 64.94783 -2.279925 4.173584 2003 151,761 101,737,445 119,047,895 159,092,173 0.1274797 63.94874 -2.059798 4.158082 2004 156,425 102,441,401 120,166,278 160,589,716 0.1301738 63.79076 -2.038885 4.155608 2005 176,080 104,113,290 122,534,825 162,270,376 0.1436980 64.16038 -1.940042 4.161386 2006 175,012 105,253,440 124,517,864 163,469,261 0.1405517 64.38730 -1.962180 4.164916 2007 186,874 105,904,192 125,808,429 164,786,302 0.1485389 64.26759 -1.906909 4.163056 2008 185,667 105,480,298 124,964,666 165,699,739 0.1485759 63.65749 -1.906659 4.153517 2009 203,877 101,483,644 120,106,722 167,119,661 0.1697470 60.72514 -1.773446 4.106358 2010 177,485 100,668,333 119,534,797 167,863,135 0.1484805 59.97048 -1.907302 4.093852 2011 160,208 101,328,629 120,445,461 168,384,994 0.1330134 60.17676 -2.017305 4.097286 2012 199,521 102,432,985 122,263,732 168,723,889 0.1631893 60.71042 -1.812844 4.106115 2013 207,956 103,388,318 123,574,162 169,356,101 0.1682847 61.04788 -1.782098 4.111659The following table shows the results of regressions on the study's data:
[1] "TABLE 8: RESULTS OF REGRESSIONS REGARDING STUDY'S 262 JOB FINDING " [1] " " [1] " JOBS CORREL " [1] " N INTERCEPT SLOPE CREATED COEF DESCRIPTION " [1] "-- --------- -------- ------- ------- -----------------------------------" [1] "2000-2007, ALL DATA" [1] " 1) -0.4284 -0.0073 -481.1 -0.0640 ln_nat_level ~ ln_imm_level + ln_imm_level2" [1] " 2) -0.3998 -0.0054 -356.0 -0.0640 ln_nat_level ~ ln_imm_level + ln_imm_level2 + fyear" [1] " 3) -0.4316 0.0021 137.3 -0.0640 ln_nat_level ~ ln_imm_level + ln_imm_level2 + fyear + floc" [1] " 4) -0.4167 0.0040 263.0 -0.0640 ln_nat_level ~ ln_imm_level + ln_imm_level2 + fyear + floc, weights=weight" [1] "USING STUDY'S FORMULA" [1] " 5) -0.4167 0.0045 293.4 -0.0640 2000-2007, study's data with corrected job count" [1] " 6) -0.5193 -0.0005 -32.2 -0.0299 2002-2005, during first span of increasing immigrant level" [1] " 7) -0.4772 -0.0036 -198.2 -0.1662 2006-2009, during second span of increasing immigrant level" [1] " 8) -0.4862 -0.0020 -121.1 -0.1111 2002-2009, during increasing immigrant level (except 2005-06)"Regressions 1 to 4 show the results of the regression after adding each additional variable. The variable fyear is a dummy variable for year, floc is a dummy variable for the state, and weight is a weight used by the study. The weight is based on the native population of each state in each year. Regression 4 is the one on which the study's 262 number is based. The calculated value was actually just under 263 and the study appears to truncate it to 262. This value, in turn, appears to be based on a truncated value for the slope of 0.004. When using the exact slope, shown to be about 0.0045 above, I came up with a calculated job gain of 293. However, regressions 6 through 9 show that when looking at periods of growth in the level of the foreign stem worker being studied, the level of native workers dropped according to the study's formula.
The following tables show the slopes obtained for all time spans of 3 or more years between 2000 and 2013 and the corresponding native gained or lost:
TABLE 9: SLOPE BETWEEN GIVEN YEARS (using same regression as was used to obtain 262 job finding) ---- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ---- Year 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 Year ---- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ---- 2000 0.0034 0.0043 0.0040 0.0038 0.0045 0.0025 0.0015 0.0018 0.0025 0.0036 0.0038 2000 2001 ....... 0.0044 0.0038 0.0036 0.0043 0.0018 0.0008 0.0012 0.0019 0.0031 0.0033 2001 2002 ....... ....... -0.0005 -0.0009 0.0005 -0.0018 -0.0020 -0.0011 -0.0002 0.0012 0.0017 2002 2003 ....... ....... ....... -0.0006 0.0001 -0.0027 -0.0027 -0.0019 -0.0008 0.0009 0.0014 2003 2004 ....... ....... ....... ....... -0.0012 -0.0035 -0.0030 -0.0022 -0.0010 0.0009 0.0013 2004 2005 ....... ....... ....... ....... ....... -0.0058 -0.0044 -0.0034 -0.0020 0.0001 0.0007 2005 2006 ....... ....... ....... ....... ....... ....... -0.0036 -0.0030 -0.0020 0.0002 0.0009 2006 2007 ....... ....... ....... ....... ....... ....... ....... 0.0002 0.0006 0.0025 0.0024 2007 2008 ....... ....... ....... ....... ....... ....... ....... ....... -0.0005 0.0015 0.0013 2008 2009 ....... ....... ....... ....... ....... ....... ....... ....... ....... 0.0019 0.0016 2009 2010 ....... ....... ....... ....... ....... ....... ....... ....... ....... ....... 0.0026 2010 TABLE 10: JOBS GAINED/LOST BETWEEN GIVEN YEARS (using same regression as was used to obtain 262 job finding but with truncation errors) ---- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ---- Year 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 Year ---- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ---- 2000 217.89 284.32 274.93 269.32 262.99 129.20 125.53 124.35 124.53 245.06 241.05 2000 2001 ....... 286.29 274.57 268.11 261.14 128.14 62.13 61.55 123.40 182.06 179.01 2001 2002 ....... ....... 0.00 -66.03 0.00 -126.06 -122.07 -60.54 0.00 59.80 117.60 2002 2003 ....... ....... ....... -62.73 0.00 -181.70 -176.36 -117.05 -59.01 58.14 57.26 2003 2004 ....... ....... ....... ....... -60.16 -178.35 -172.89 -115.00 -58.15 57.31 56.45 2004 2005 ....... ....... ....... ....... ....... -348.87 -225.22 -169.11 -114.48 0.00 55.60 2005 2006 ....... ....... ....... ....... ....... ....... -222.57 -167.55 -113.87 0.00 55.19 2006 2007 ....... ....... ....... ....... ....... ....... ....... 0.00 56.32 110.86 109.06 2007 2008 ....... ....... ....... ....... ....... ....... ....... ....... 0.00 55.18 54.18 2008 2009 ....... ....... ....... ....... ....... ....... ....... ....... ....... 109.54 107.33 2009 2010 ....... ....... ....... ....... ....... ....... ....... ....... ....... ....... 164.18 2010 TABLE 11: NATIVE JOBS GAINED/LOST PER EACH 100 STEM WORKERS WITH ADVANCED US DEGREES BETWEEN GIVEN YEARS (using study's methodology with no errors) ---- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ---- Year 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 Year ---- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ---- 2000 245.51 306.94 274.79 257.13 293.44 158.33 96.35 112.38 154.98 221.82 225.99 2000 2001 ....... 317.81 262.67 242.41 280.19 114.42 46.88 73.19 117.79 188.00 194.49 2001 2002 ....... ....... -32.21 -59.12 30.37 -110.55 -121.07 -65.43 -12.20 74.36 98.75 2002 2003 ....... ....... ....... -39.24 3.18 -162.83 -161.62 -108.66 -47.03 50.47 78.46 2003 2004 ....... ....... ....... ....... -70.56 -206.88 -175.46 -125.54 -57.93 52.45 72.69 2004 2005 ....... ....... ....... ....... ....... -338.56 -249.66 -189.44 -114.91 4.97 41.33 2005 2006 ....... ....... ....... ....... ....... ....... -198.23 -168.66 -115.45 8.89 50.58 2006 2007 ....... ....... ....... ....... ....... ....... ....... 13.27 33.91 136.92 132.92 2007 2008 ....... ....... ....... ....... ....... ....... ....... ....... -27.36 82.76 73.07 2008 2009 ....... ....... ....... ....... ....... ....... ....... ....... ....... 101.55 83.93 2009 2010 ....... ....... ....... ....... ....... ....... ....... ....... ....... ....... 142.78 2010 # value is 262.99 if the slope is truncated. * value is 293.44 if the slope is not truncated.As with the H-1B data, the table above shows that when one looks at a time span for which the foreign worker being studied is increasing, a loss of native jobs is indicated. For example, 2002 to 2009 shows an steady increase in such workers and their share of the employment pool was generally increasing. The table, however, shows a negative slope of -0.0020 during this period, indicating a loss of native jobs.
The following table shows the p-values that correspond to the slopes in the prior tables:
TABLE 12: P-VALUE OF REGRESSION SLOPE BETWEEN GIVEN YEARS (using study's methodology) ---- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ---- Year 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 Year ---- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ---- 2000 0.1144 0.0206 0.0307 0.0492 0.0141 0.1631 0.3987 0.3366 0.1956 0.0487 0.0313 2000 2001 ....... 0.0425 0.0685 0.0993 0.0330 0.3439 0.6955 0.5476 0.3426 0.1038 0.0688 2001 2002 ....... ....... 0.8532 0.7291 0.8360 0.3923 0.3364 0.6081 0.9247 0.5321 0.3633 2002 2003 ....... ....... ....... 0.8374 0.9840 0.2334 0.2242 0.4175 0.7269 0.6815 0.4818 2003 2004 ....... ....... ....... ....... 0.7145 0.1782 0.2313 0.3912 0.6894 0.6844 0.5275 2004 2005 ....... ....... ....... ....... ....... 0.0544 0.1336 0.2368 0.4618 0.9707 0.7241 2005 2006 ....... ....... ....... ....... ....... ....... 0.2731 0.3076 0.4641 0.9470 0.6584 2006 2007 ....... ....... ....... ....... ....... ....... ....... 0.9417 0.8395 0.3188 0.2376 2007 2008 ....... ....... ....... ....... ....... ....... ....... ....... 0.8900 0.5667 0.5138 2008 2009 ....... ....... ....... ....... ....... ....... ....... ....... ....... 0.4249 0.4028 2009 2010 ....... ....... ....... ....... ....... ....... ....... ....... ....... ....... 0.2039 2010In the above table, the p-values are colored red if they are less than 0.01 (p < 0.01), orange if they are less than 0.05 (0.01 <= p < 0.05), and green if they are less than 0.1 (0.05 <= p < 0.1). As can be seen, there are no red values of the highest significance but there 8 and 4 of the other two levels, respectively. There is at least one span, 2005 to 2008, that has a p-value less than 0.1 but corresponds to native jobs losses of 348.87 and 338.56 in the prior two tables.
In any event, these numbers show how critical the first and last year of the chosen time span are to the results. This seems to be especially true for certain years such as the tech crash that occurred in 2000-2002. As can be seen in the first table in this section, there was a steep job loss for both foreign and native workers during this period. This underlines an interesting fact. A job increase for both foreign and native workers will result in a regression finding a positive association between the two. However, a steep job loss will result in a regression finding a similar positive association. Since time is not included in the plot, both cases are essentially identical from a mathematical point of view. Of course, the study is not claiming that foreign job LOSSES lead to native job LOSSES. Hence, it makes sense to focus on periods of gains in the jobs of foreign workers. As mentioned above, when looking at periods of growth in the level of the foreign stem worker being studied, the level of native workers generally dropped according to the study's formula.
The following table shows the standard errors that correspond to the slopes in the prior tables:
STANDARD ERROR OF REGRESSION SLOPE BETWEEN GIVEN YEARS (using study's methodology) ---- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ---- Year 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 Year ---- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ------- ---- 2000 0.0021 0.0018 0.0018 0.0019 0.0018 0.0018 0.0018 0.0019 0.0019 0.0018 0.0017 2000 2001 ....... 0.0022 0.0021 0.0022 0.0020 0.0019 0.0019 0.0020 0.0020 0.0019 0.0018 2001 2002 ....... ....... 0.0026 0.0026 0.0023 0.0020 0.0021 0.0021 0.0021 0.0020 0.0018 2002 2003 ....... ....... ....... 0.0030 0.0026 0.0022 0.0023 0.0023 0.0023 0.0021 0.0019 2003 2004 ....... ....... ....... ....... 0.0032 0.0026 0.0025 0.0025 0.0025 0.0022 0.0020 2004 2005 ....... ....... ....... ....... ....... 0.0030 0.0029 0.0028 0.0027 0.0024 0.0021 2005 2006 ....... ....... ....... ....... ....... ....... 0.0032 0.0029 0.0028 0.0024 0.0021 2006 2007 ....... ....... ....... ....... ....... ....... ....... 0.0033 0.0030 0.0025 0.0021 2007 2008 ....... ....... ....... ....... ....... ....... ....... ....... 0.0035 0.0026 0.0021 2008 2009 ....... ....... ....... ....... ....... ....... ....... ....... ....... 0.0023 0.0019 2009 2010 ....... ....... ....... ....... ....... ....... ....... ....... ....... ....... 0.0020 2010As can be seen, the standard error is between 0.0017 and 0.0022 in the first two rows that correspond to job gains and between 0.0017 and 0.0033 when including all of the spans that correspond to job gains. This compares to 0.0020 and 0.0035 for those spans that correspond to job losses, a relatively small difference.
Source Code for R Programs Used in this Analysis